This is the first of three blog posts on the basics of representation learning in machine learning:

What Is Representation Learning?
Why Use Representation Learning? (not published yet)
Methods Of Representation Learning (not published yet)

1. Intro

Representation learning (or synonymously feature learning) is a widely used term in machine learning, yet it is ill-defined and rarely explained. This series of posts provides an introduction for students and researchers who are new to the field.

In this first post, I am going to shed some light on how representation learning has been described in the literature up to today. By deriving a definition of a representation of a data set, I suggest a definition of representation learning (in machine learning) that is more encompassing than existing descriptions. Finally, I will set representation learning into the context of related but different topics.

Some terminology around representation learning is commonly used across the literature. Besides representation and representation learning, I will also use this post to explain the meaning (in the context of machine learning) of:

Feature, feature space, latent space
Learning, downstream task
Manifold, embedding
Feature learning, feature selection, feature construction, feature extraction, feature engineering

2. Descriptions in Literature

Certainly the most famous paper on representation learning is “Representation Learning: A Review and New Perspectives” by Bengio et al., 2013 [1]. It has been cited more than 10,000 times. In it, Bengio states

This paper is about representation learning, i.e., learning representations of the data that make it easier to extract useful information when building classifiers or other predictors.

This description is somewhat circular, but makes an interesting point: It focuses on the purpose of representation learning (the why) rather than the process (the how). Bengio does not state it explicitly, but that focus is justified by the large amount of different methods which can be used for representation learning.

In the introduction of his paper, Bengio equates the word representation to features (the variables or dimensions of a data point). This is also important since defining representation is the first step to defining representation learning.

A more rigorous definition of representation learning is provided by Le-Khac et al. [2]:

Representation learning refers to the process of learning a parametric mapping from the raw input data domain to a feature vector or tensor, in the hope of capturing and extracting more abstract and useful concepts that can improve performance on a range of downstream tasks.

Le-Khac’s definition shares the emphasis on solving downstream tasks with Bengio’s description. While Bengio (albeit briefly) explains what a representation is, Le-Khac focuses more on the learning aspect: One learns a parametric mapping from raw input to representation.

Last but not least, Zhang et al. [3] provide a mathematical definition specifically of network representation learning – i.e. representation learning on network data (that’s Definition 6 in the paper, not cited here). Their definition also speaks of learning a mapping and is in this regard similar to Le-Khac’s. Zhang additionally states that the mapping should preserve information by preserving similarities between instances.

Bengio’s and Le-Khac’s descriptions of the term representation learning are brief and mentioned in passing. Zhang’s definition is more deliberate, but specific to a certain kind of data. All three are merely stated rather than derived, and are not further explained or discussed. Building on their work, I will derive a definition and discuss its implications in the remainder of this blog post.

3. Representations

To understand the term representation learning, we first have to understand what a representation is and what it means to learn one. In this section, I will define representation in the context of machine learning.

When we speak of a representation in the context of machine learning, we think of data instances (images, words, graphs, …) as vectors in some vector space – quite like those in Figure 1.

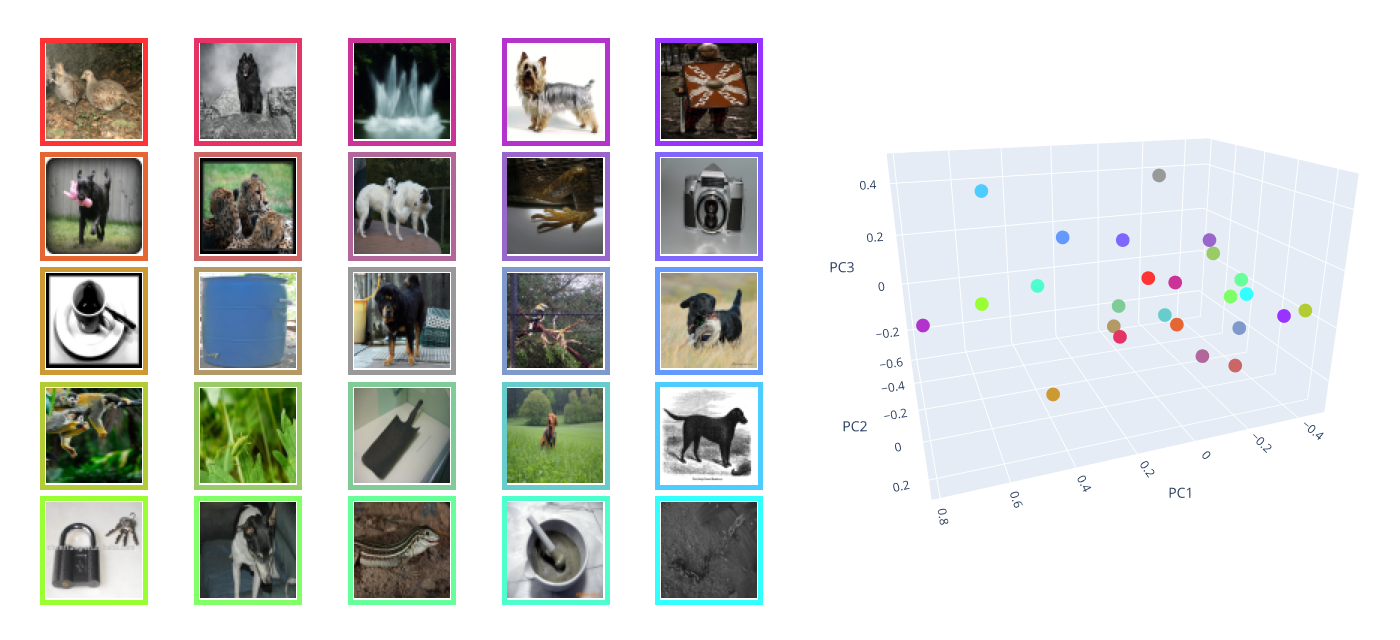
Fig 1: A few random imagenet pictures, color-coded with rectangles, mapped into 3d space with PCA.

In the interest of generalizability, let’s go one step back from vector spaces. A vector space implies order and continuity, which a data feature that encodes names, for instance, would not have. Instead, I am going to talk of feature spaces. A feature space contains the set of all data instances that can be expressed in terms of its features. Since the features can be seen as random variables, the feature space can mathematically be considered a probability space. If you find this idea of a feature space too abstract, just continue thinking of vector spaces whenever I write feature space. Most feature spaces (and certainly those in Figure 1) are a vector space, after all.

All data can be expressed through some set of features, and data instances in the same representation share the same feature space. It thus makes sense to call the feature space itself representation.

Additionally, a representation requires a mapping from an original feature space to a new feature space. Let’s call the latter latent space in line with the probabilistic perspective assumed above. Much of the representation learning literature uses this term, too. Without the mapping between both spaces, the data instances in latent space do not represent anything at all – they would just be points without a meaning. In Figure 1, the mapping is visualized by colors. Without the colours, the two feature spaces in the figure would not be connected and there would be no representation.

With all this in mind, it’s possible to define representation:

Definition: Representation

A representation in machine learning is a feature space \(S_{latent}\) that is connected through some mapping \(f: S_{original} \rightarrow S_{latent}\) to a feature space \(S_{original}.\)

This definition agrees with, and extends, Bengio’s description of a representation as a set of features.

Hidden behind this paragraph is a list of more specific considerations on the nature of \(f\). They are not important to understand representation learning or the remainder of this post, but provide some more context about my definition of representation. Click to expand.

Direction of \(f\!:\) Does it make more sense to define \(f\) as a map \(S_{latent} \rightarrow S_{original}\) or as the opposite \(S_{original} \rightarrow S_{latent}?\) The former makes sense when latent points are already given: A known map to \(S_{original}\) then provides them with meaning. The latter, however, makes sense in the context of representation learning where a representation, including a mapping from \(S_{original}\) to \(S_{latent},\) first has to be found. In my opinion, both are valid choices. Since we are considering representation learning here, I have decided to go with the second option for the definition.
Properties of \(f\!:\) Is \(f\) injective (no two original data points can be represented by the same latent point) or surjective (every point in latent space has to represent a point in original space)? Not necessarily (and in fact it's usually not): A large subset of representation learning methods perform dimensionality reduction, which violates injectivity. Others perform dimensionality expansion which violates surjectivity, so the mapping does not have to be either.
Mapping whole features: Generally speaking, \(f\) maps individual instances in features space \(S_{original}\) to individual instances in feature space \(S_{latent}.\) A subset of potential mappings are those that consistently map features of \(S_{original}\) to features in \(S_{latent}\) independent of the values those features take. Linear methods such as PCA do this. If the mapping is not too complex, it will result in an interpretable representation. Still, mapping features to features proves to be quite a restriction and powerful non-linear methods like neural networks consequently don't do it.

What is a good representation?

All three papers I mentioned so far propose properties of good representations. I recommend taking these with a grain of salt. While the properties will be beneficial in most settings, they might be detrimental in others.

There is one list compiled by Bengio, which Le-Khac has reiterated in his paper. Zhang provides his own distinct list of good properties.

Bengio and Le-Khac state that a good representation is

Smooth - The latent space should be well-behaved enough to allow e.g. for interpolation
Distributed/expressive - Each dimension of a representation should exponentially increase its expressiveness (this is not the case for e.g. one-hot encoding)
Disentangled - The individual dimensions should contain distinct factors of variation in the data instead of being correlated (see [4] for an interesting discussion on this)
Abstract - The representation should be invariant to irrelevant changes in the input

Zhang as well as Bengio say that a good representation is

Informative - A representation should include all relevant information from the original data
Low-dimensional - More specifically of lower dimensionality than the original data

Zhang suggests that a good representation is additionally

Continuous - Many downstream methods supposedly require continuous input

There are of course counterexamples. Ota et al. [5], for instance, expand rather than shrink the feature space to gain superior performance in reinforcement learning. The widely cited VQ-VAE by Oord et al. [6] creates discrete representations. Nevertheless, the vast majority of representation learning does try to enforce those properties suggested by Bengio and Zhang.

In the end each task imposes its own requirements on a representation. For specific cases, it is best to derive useful properties directly from the objective posed by a given task.

4. Definition

Now that we know what a representation is, we still need to define learning. In the context of machine learning, it makes sense to think of learning as the automated process of optimizing some mapping \(f_\theta: x_{input} \mapsto x_{output}\) for data instances \(x.\) A parameterized mapping allows to map future data instances from original to latent feature space. Without parameterization, the representation would merely be calculated and not learned.

Combining this concept of learning with above definition of representation, however, does still not go beyond regular machine learning. Since representation learning is not synonymous to machine learning, a further component is required to distinguish the two: The downstream task(s). As opposed to e.g. class labels, a representation is not an end in itself but an intermediate step for improving performance in downstream tasks.

This raises the question: What exactly is a downstream task? That’s not a trivial question, and authors usually don’t define the term, or consider only a specific task in their publication. It seems natural to consider classification or regression downstream tasks. Beyond this, I would argue that any form of decision making (e.g. image segmentation, language generation or acting in a reinforcement learning environment) is a downstream task as well. So is data analysis (by either a human or a machine).

Putting all aspects together, it becomes possible to define representation learning:

Definition: Representation Learning

Representation learning is the automated process of optimizing parameters \(\theta\) of a mapping \(f_\theta: S_{original} \rightarrow S_{latent}\) from feature space \(S_{original}\) to representation \(S_{latent},\) in order to improve performance on one or more downstream tasks.

The definition agrees with Le-Khac’s on the parametric mapping. The requirement of being useful for downstream tasks is also in agreement with both Bengio and Le-Khac.

It does however avoid the circularity of Bengio’s description and is more encompassing than Le-Khac’s because it does not restrict potential properties of latent spaces and representations.

Hidden behind this paragraph is a section which explains the terms embedding and manifold, and relates them to above definition. They are not important to understand representation learning or the remainder of this post, but are often used in the literature with their meaning not always obvious. Click to expand.

Embeddings and Manifolds

Bengio provides this explanation of the terms embedding, manifold, and their relevance:

Real-world data presented in high dimensional spaces are expected to concentrate in the vicinity of a manifold \(\mathcal{M}\) of much lower dimensionality \(d_\mathcal{M}\) , embedded in high dimensional [original] space \(\mathbb{R}^{d_x}\). This prior seems particularly well suited for AI tasks such as those involving images, sounds or text, for which most uniformly sampled input configurations are unlike natural stimuli. [...] With this perspective, the primary [representation] learning task is then seen as modeling the structure of the data-supporting manifold.

Effectively, this means that most data contained in a feature space (i.e. data that can be expressed in terms of the features) is not realistic data. This is increasingly likely for larger feature spaces. Requiring representation learning to model the structure of the relevant manifold(s) basically means creating low-dimensional, informative representations; two of the desirable properties from above.

Now, how do they connect to our definition? In mathematics, a manifold is a locally Euclidean topological space. An embedding is an injective map that places a structure inside another. Confusingly, the former structure itself – in our case the manifold – is also sometimes called embedding.

In our definition, \(S_{latent}\) would thus be an embedded manifold if it is a subspace (with a possibly different topology) of \(S_{original}.\) The embedding which connects the two is not \(f_\theta,\) but a hypothetical function \(g: S_{latent} \rightarrow S_{original}\) that maps each latent point to a distinct point in original space, quite like the (not necessarily injective) decoder of an autoencoder does.

Within the machine learning community, however, the word embedding generally refers to the manifold rather than the map. Learning an embedding then means learning a feature space. In my opinion this is unfortunate (albeit widespread) wording, as what is actually learned are parameters of the function \(f_\theta\) which, as we have seen, is not in fact an embedding.

Regardless of specific wording, the idea of embeddings of manifolds can motivate the use of representation learning and justify certain properties of representations.

5. Examples

The main reason to fix a definition for representation learning is to understand which methods learn representations and which don’t. This in turn makes it possible to create an overview of the field, like the (non-comprehensive) one I provide in #3 of this series of blog posts. But before looking at an entire overview, let’s investigate the definition by looking at some examples that are or are not representation learning.

PCA

This a straightforward example of representation learning, also mentioned as such in [1, Section 5]. Principle component analysis is a well-known method that learns a linear transformation of a vector space. A linear transformation is a parameterized mapping. PCA can be used to decorrelate features and potentially discard those with low variance. Both properties can improve performance on downstream tasks, be it machine learning tasks or for instance data analysis.

CNN

A classical convolutional neural network that classifies images is, in itself, not an instance of representation learning as the predicted labels are not further used to improve performance on downstream tasks. Predicting the labels already is the task. However, the CNN does representation learning internally by hierarchically abstracting the input features layer by layer. The convolutional layers are a parameterized function, and their output is used to simplify the subsequent task of classification (which, one could argue, is performed by the last layer). Charte et al. [7, Section 2.2], for instance, come to a similar conclusion.

t-SNE

The classical t-SNE dimensionality reduction method is not representation learning. It does transform data in an automated way by calculating similarity between given data points and reconstructing this similarity in lower dimensional space. This means it merely projects data points instead of learning a parameterized function and is hence incapable of transforming future data points. One could say it calculates rather than learns a representation.

Besides representation learning, there are a range of closely related concepts and keywords:

Feature learning, feature selection, feature extraction, feature construction, and feature engineering.

These are not coherently treated as distinct and unambiguous concepts across the literature, but the overall schematic I present here should at least provide a rough guideline through the jungle of conflicting terminology. Figure 2 visualizes their relationship to each other.

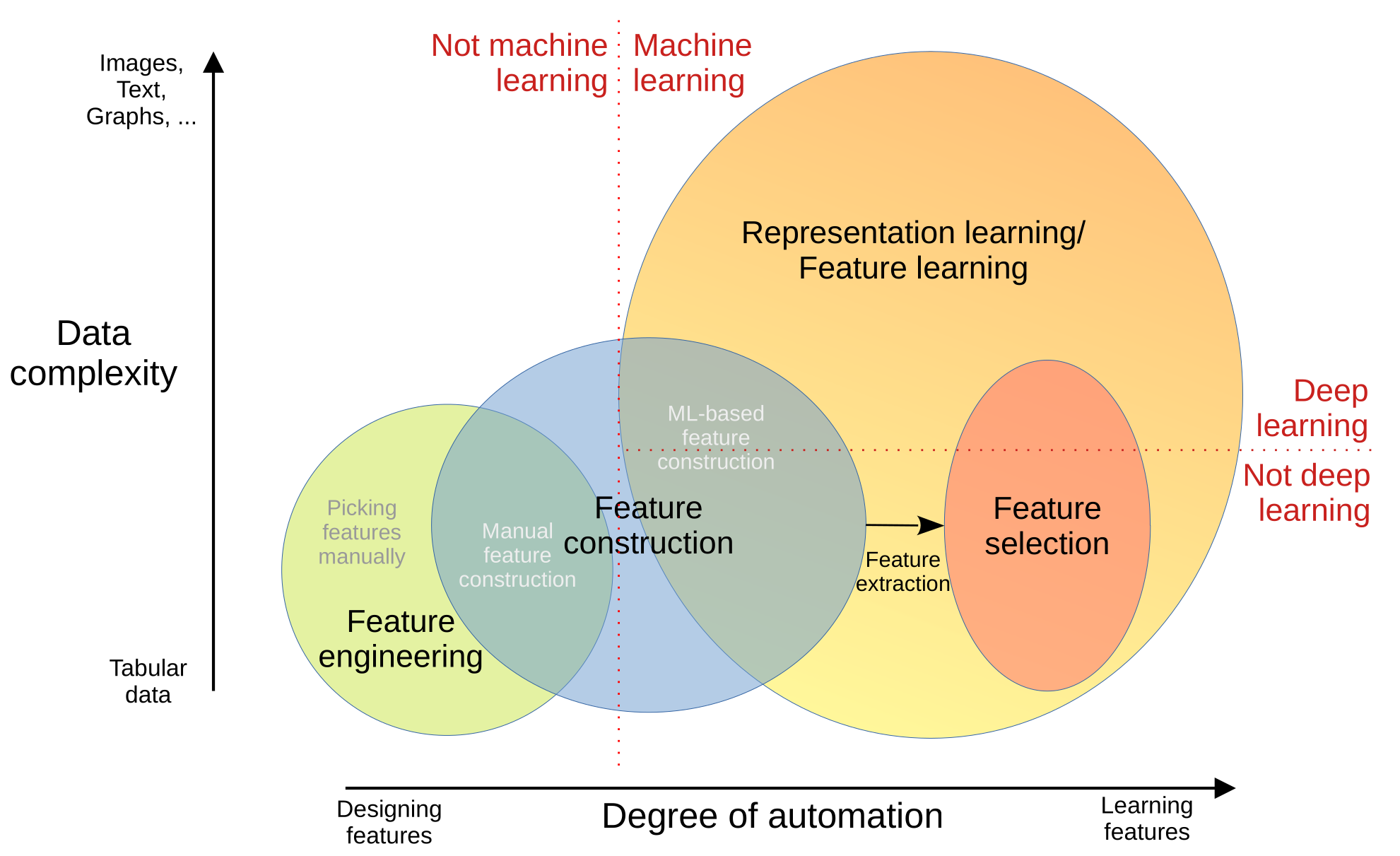
Fig 2: Rough schematic of topics related to representation learning. Feature construction followed by feature selection is called feature extraction.

Feature learning

Feature learning is a somewhat older term, but used synonymously to representation learning in many publications. It was used even before deep learning became successful on a large scale. The term representation learning on the other hand only started to be used in the 2010s with the advent of deep learning. Nowadays, both terms are equally used – some papers mention either one or the other, others even use both interchangeably (e.g. [1], [8], [9]).

Feature selection

Feature selection, as opposed to feature learning, is clearly distinct from from representation learning. It describes the process of using machine learning methods for selecting a subset of features from a given set [10], which makes it a subfield of representation learning. Feature selection is a research field that has been around for many years, yet is still actively researched as there are many application areas, such as gene analysis, where only a few features from a large set hold most or even all relevant information [11].

Feature extraction/construction

Feature extraction describes the process of constructing features (feature construction) – usually this means expanding the dimensionality of some original data in either an automated or manual way – and then selecting a subset thereof through feature selection [12]. Feature extraction is an instance of representation learning only if all steps are using machine learning methods. The rather cumbersome process of feature extraction has however lost popularity as neural networks offering all-in-one solutions gained pace in representation learning.

Feature engineering

Feature engineering, finally, is the process of manually constructing or selecting features. As it lacks automation, it is not representation learning. Nevertheless, feature engineering is a noteworthy alternative to representation learning. It is mostly used for simple tabular data – especially in applications where domain knowledge provided by human experts is important.

References

Y. Bengio, A. Courville, and P. Vincent, “Representation Learning: A Review and New Perspectives”, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 35, no. 8, pp. 1798–1828, Aug. 2013, doi: 10.1109/TPAMI.2013.50.
P. H. Le-Khac, G. Healy, and A. F. Smeaton, “Contrastive Representation Learning: A Framework and Review”, IEEE Access, vol. 8, pp. 193907–193934, 2020, doi: 10.1109/ACCESS.2020.3031549.
D. Zhang, J. Yin, X. Zhu, and C. Zhang, “Network Representation Learning: A Survey”, IEEE Transactions on Big Data, vol. 6, no. 1, pp. 3–28, Mar. 2020, doi: 10.1109/TBDATA.2018.2850013.
F. Locatello et al., “Challenging Common Assumptions in the Unsupervised Learning of Disentangled Representations”, arXiv:1811.12359 [cs, stat], Jun. 2019.
K. Ota, D. K. Jha, and A. Kanezaki, “Training Larger Networks for Deep Reinforcement Learning”, arXiv: 2102.07920 [cs] Feb. 2021.
A. van den Oord, O. Vinyals, and K. Kavukcuoglu, “Neural Discrete Representation Learning”, arXiv: 1711.00937 [cs], May 2018.
D. Charte, F. Charte, M. J. del Jesus, and F. Herrera, “An analysis on the use of autoencoders for representation learning: Fundamentals, learning task case studies, explainability and challenges”, Neurocomputing, vol. 404, pp. 93–107, Sep. 2020, doi: 10.1016/j.neucom.2020.04.057.
X. Chen, Y. Duan, R. Houthooft, J. Schulman, I. Sutskever, and P. Abbeel, “InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets”, arXiv: 1606.03657 [cs, stat], Jun. 2016.
A. Grover and J. Leskovec, “node2vec: Scalable Feature Learning for Networks”, in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, Aug. 2016, pp. 855–864. doi: 10.1145/2939672.2939754.
G. Chandrashekar and F. Sahin, “A survey on feature selection methods”, Computers & Electrical Engineering, vol. 40, no. 1, pp. 16–28, Jan. 2014, doi: 10.1016/j.compeleceng.2013.11.024.
J. Li et al., “Feature Selection: A Data Perspective”, ACM Comput. Surv., vol. 50, no. 6, p. 94:1-94:45, Dec. 2017, doi: 10.1145/3136625.
I. Guyon, S. Gunn, M. Nikravesh, and L. A. Zadeh, “Feature Extraction: Foundations and Applications”. Springer, 2008.